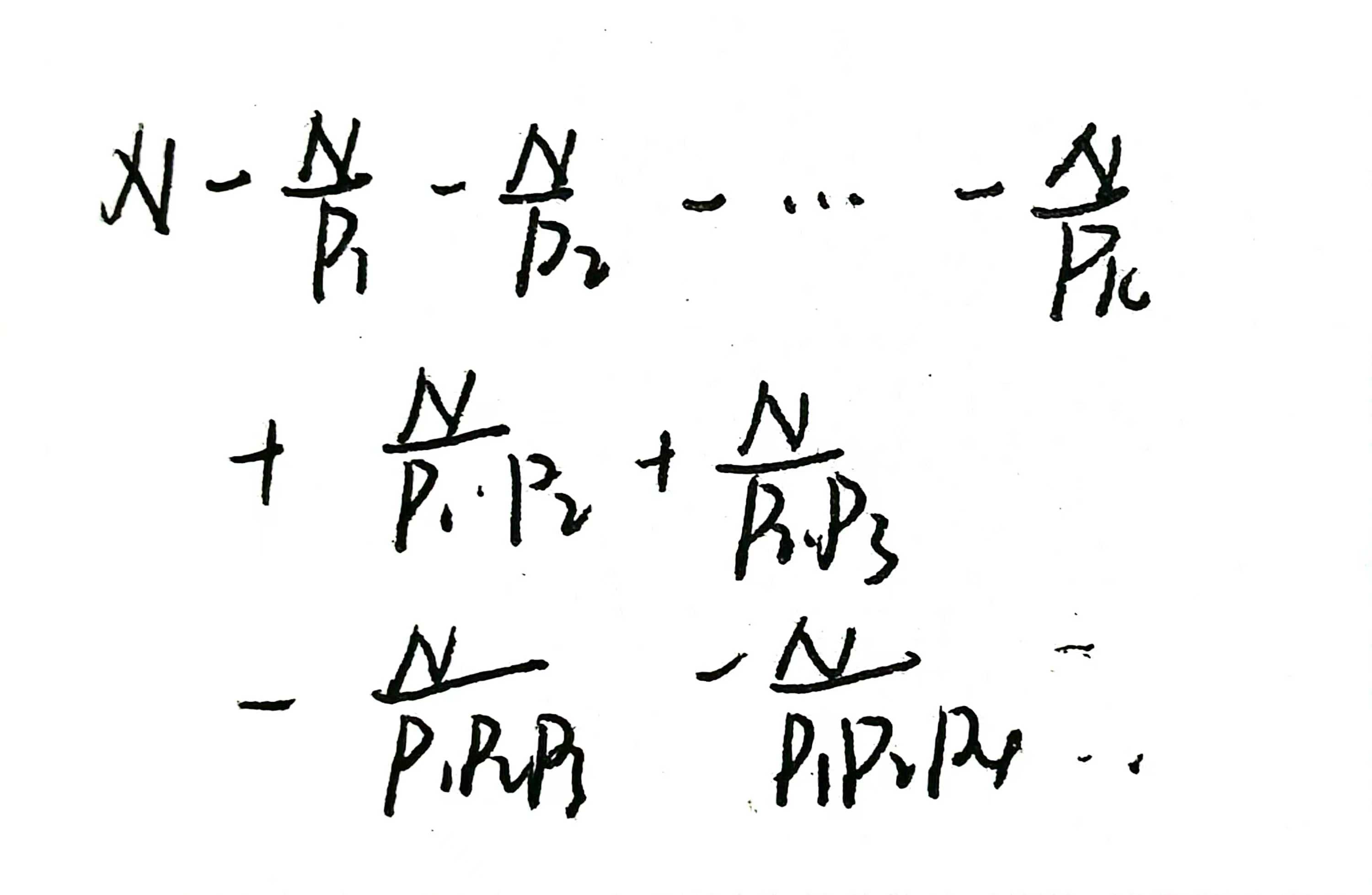质数的判定

试除法判定质数

==质数==：对于＞1的整数，如果只包含1和本身这两个约束，就被称为质数或者素数

O(sqrt(n))

1
2
3
4
5
6
7
8
9
bool prime(int x){
    if(x<2) return false;//判断是否>1
    else{
        for(int i=2;i<=x/i;i++){
            if(x%i==0) return false;
        }
    }
    return true;
}

分解质因数

从小到大枚举所有数

O(sqrt(n))

1
2
3
4
5
6
7
8
9
10
11
12
void quite(int x){
    int n=x;
    for(int i=2;i<=n/i;i++){//n中最多只包含一个>qprt(n)的质因子
        int s=0;
        while(x%i==0){//i一定是质数
            s++;
            x=x/i;
        }
        if(s!=0) cout<<i<<" "<<s<<endl;
    }
    if(x>1) cout<<x<<" 1"<<endl;//>qprt(n)的质因子
}

筛质数

从前往后，把每一个数的倍数筛掉

1
2
3
4
5
6
7
8
9
10
11
12
13
void prime(){
    if(n<2) cnt=0;
    else {
        for(int i=2;i<=n;i++){
            if(!st[i]){
                cnt++;
                for(int j=i;j<=n;j+=i){
                    if(!st[j]) st[j]=true;
                }
            }
        }
    }
}

<埃氏筛法>优化：只有是质数，才需要筛掉倍数

质数定理：1~n中有（n/lnn)个质数

时间复杂度：（n*lnn/lnn)=n

核心：只会被最小的质因子筛掉

1
2
3
4
5
6
7
8
9
10
11
12
13
void prime(){
    if(n<2) cnt=0;
    else {
        for(int i=2;i<=n;i++){
            if(!st[i]) primes[cnt++]=i;
            for(int j=0;primes[j]<=n/i;j++){//从小到大枚举所有质数
                st[primes[j]*i]=true;
                //cout<<primes[j]<<" "<<j<<" "<<i<<endl;
                if(i%primes[j]==0) break;//p[j]一定是i的最小质因子，p[j]一定是p[j]*i的最小质因子
            }//if(i%primes[j]!=0)，则p[j]一定小于i的最小质因子，p[j]一定是p[j]*i的最小质因子
        }
    }
}
1
2
3
1.if(i%primes[j]==0),p[j]一定是i的最小质因子，p[j]一定是p[j]*i的最小质因子
2.if(i%primes[j]!=0)，则p[j]一定小于i的最小质因子，p[j]一定是p[j]*i的最小质因子
3.对于任何一个合数，假设pj是x的最小质因子，当i枚举到x/pj的时候一定会被筛掉

约数

试除法求一个数的所有约数

1
2
3
4
5
6
7
8
9
10
11
12
void yy(int x){
    vector<int> res;
    for(int i=1;i<=x/i;i++){
        if(x%i==0){
            res.push_back(i);
            if(i!=x/i) res.push_back(x/i);
        }
    }
    sort(res.begin(),res.end());
    for(auto t:res) cout<<t<<" ";
    cout<<endl;
}

约数个数

int范围内，约数个数最多的是1500个左右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
int main(){
    int n;
    cin>>n;
    unordered_map<int,int> primes;
    while(n--){
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++){
            while(x%i==0){
                primes[i]++;
                x=x/i;
            }
        }
        if(x>1) {
            primes[x]++;
            }
    }
    LL res=1;
    for(auto prime:primes) res=res*(1+prime.second)%mod;
    cout<<res;
    return 0;
}

约数之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
int main(){
    int n;
    cin>>n;
    unordered_map<int,int> primes;
    while(n--){
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++){
            while(x%i==0){
                primes[i]++;
                x=x/i;
            }
        }
        if(x>1) {
            primes[x]++;
            }
    }
    LL res=1;
    LL t=1;
    for(auto prime:primes)
    {
        t=1;
        int p=prime.first;//底数
        int a=prime.second;//指数
        while(a--){
            t=(t*p+1)%mod;
        }
        res=res*t%mod;
    }
    cout<<res;
    return 0;
}

最大公约数（欧几里得算法/辗转相除法）

if(d|a&&d|b) ->d|(a+b)

(a,b)=(b,a mod b)

1
2
3
证明：若d|a,且d|(a-c*b)
则d|(a-c*b+c*b)
则d|a

因此，左边的最大公约数=右边的最大公约数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
#include<algorithm>
using namespace std;
int gcb(int a,int b){
    return b ? gcb(b,a%b):a;//b如果不是0，返回gcb(b,a%b)
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int a,b;
        cin>>a>>b;
        cout<<gcb(a,b)<<endl;
    }
    return 0;
}

欧拉函数

欧拉函数的定义：

1~N中和N互质的个数

  1. 从1~N中去掉p1,p2,…,pk的倍数
  2. 加上所有pi*pj的倍数
  3. 减去所有pi*pj*pk的倍数
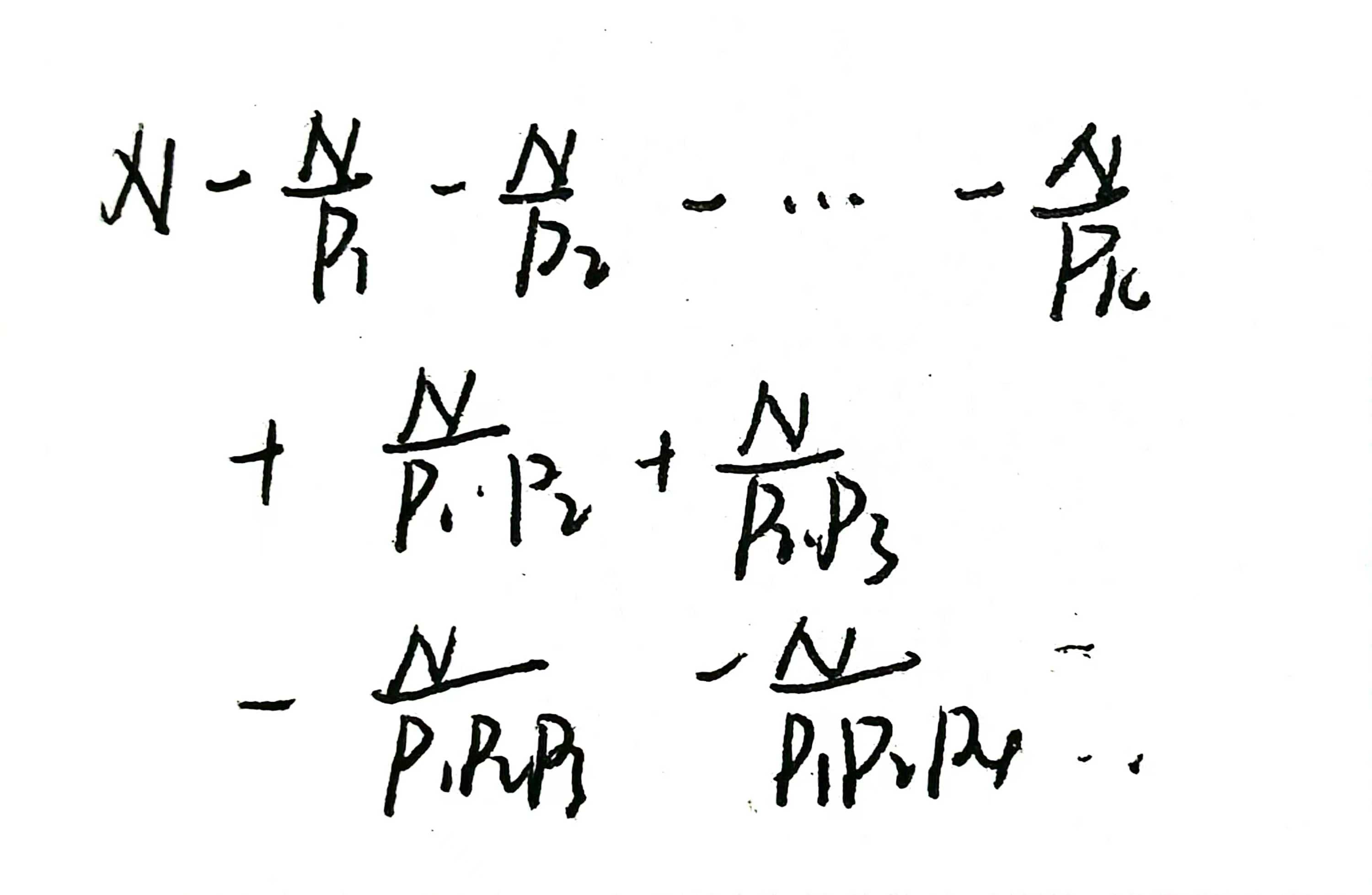
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        int res=x;
        for(int i=2;i<=x/i;i++){
            if(x%i==0){//i是质因子
                res=res/i*(i-1);
                x=x/i;
                while(x%i==0){
                    x=x/i;
                }
            }
        }
        if(x>1) res=res/x*(x-1);//还有一个质因子
        cout<<res<<endl;
    }
    return 0;
}

筛法求欧拉函数

求1~n中每个数的欧拉函数

O(n)时间复杂度下求得

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
long long pri(int x){
    phi[1]=1;//1到1中和1互质的数只有1
    int cnt=0;
    for(int i=2;i<=x;i++)
    {
        if(!st[i]) {//质数
            primes[cnt++]=i;
            phi[i]=i-1;//如果p是质数，那么1~p中又p-1个质数
        }
        for(int j=0;primes[j]<=x/i;j++){//枚举所有的质数
                st[i*primes[j]]=true;
            if(i%primes[j]==0) {//pj是i的一个质因子
                phi[primes[j]*i]=primes[j]*phi[i];//pj是i的一个质因子，因此phi[i]已经有了一个(1-1/pj)
                break;
            }
            phi[primes[j]*i]=(primes[j]-1)*phi[i];//i%pj!=0,则pj为i*pj的一个最小质因子，
        }
    }
    long long res=0;
    for(int i=1;i<=x;i++) res+=phi[i];
    return res;
}

快速幂

预处理：a^1^modp ,a^2^modp ,a^4^modp ,a^8^modp ……a^(2^log2k^)modp

每一个数都是上一个数的平方modp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int pi(int a,int k,int p){
    int  res=1;
    while(k){
        if(k&1==1)
        {
            res=(LL)res*a%p;
        }
        k=k>>1;
        a=(LL)a*a%p;
    }
    return res;
}
int main(){
    int a,k,p;
    int n;
    cin>>n;
    while(n--){
        scanf("%d%d%d",&a,&k,&p);
        printf("%d\n",pi(a,k,p));//a^k mod p
    }
    return 0;
}

快速幂求逆元

==乘法逆元==：

找到x，使得b*x%m=1

比如，3*x%5==1,2是3的模5逆元，3^5-2^%5=2,可以求出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int pi(int a,int k,int p){
    int  res=1;
    while(k){
        if(k&1==1)
        {
            res=(LL)res*a%p;
        }
        k=k>>1;
        a=(LL)a*a%p;
    }
    return res;
}
int main(){
    int a,k,p;
    int n;
    cin>>n;
    while(n--){
        scanf("%d%d",&a,&p);
        if(a%p){
            printf("%d\n",pi(a,p-2,p));
        }
        else puts("impossible");//误解
    }
    return 0;
}

扩展欧几里得算法

裴蜀定理：

​ 对于任意一对正整数a,b,那么一定存在整数x,y，使得ax+by=(a,b)–a,b的最大公约数（x,y是最小的正整数）

（a,b)=(b,a%b)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<iostream>
#include<algorithm>
using namespace std;
int exgcd(int a,int b,int &x,int &y){
    if(!b){//0和a的最大公约数一定是a
        x=1,y=0;
        return a;
    }
    else{
        int d=exgcd(b,a%b,y,x);//by+(a%b)x=(b,a%b)=(b,a)=by+(a-a/b*b)x,
        y-=(a/b)*x;//ax+b(y-a/b*x),所以x不变，y变成y-a/b*x
        return d;
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    while(n--){
        int a,b,x,y;
        scanf("%d%d",&a,&b);
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
    return 0;
}

中国剩余定理

m1,m2,……两两互质

给定一堆互质的数，使得
x%m1=a1
x%m2=a2
x%m3=a3
x%m4=a4

M=m1*m2*…*mk
Mi=M/mi(即除了mi之外所有的乘积)

Mi^-1^表示Mi模mi的逆,用扩展欧几里得算法求，等价于ax%m=1

x=a1M1M1^-1^+a2M2M2^-1^+a3M3M3^-1^+…+akMkMk^-1^

高斯消元

在n^3^时间复杂度内，求解n个未知数的n个一元线性方程组：

a11x1+a12x2+a13x3+…+a1nxn+=b1
a21x1+a22x2+a23x3+…+a2nxn+=b2
…
an1x1+an2x2+an3x3+…+annxn+=bn

==解==：
无解：0=b
无穷多组解：方程数<未知数的个数
唯一解：完美阶梯型

==做法==（初等行列变换）枚举每一列：

​ 找到绝对值最大的一行
​ 将该行换到最上面
​ 把该行的第一个数变成1
​ 把下面所有行的第c列消成0

可以变成上三角的形式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const int N=110;
const double egg=1e-6;//C++浮点数存储有误差，如果小于一个数就可以认为是0
double a[N][N];
int r=0,n;
void out()
{
    for(int i=0;i<n;i++){
        for(int j=0;j<=n;j++){
            printf("%.2lf ",a[i][j]);
            
        }
        puts("");
    }
    puts("");
}
int gause(){
    for(int c=0;c<n;c++){
        int t=r;
        for(int i=t;i<n;i++){
            if(fabs(a[t][c])<fabs(a[i][c])) t=i;//找到这一列的最大值，fabs:返回浮点数的绝对值
        }
        if(fabs(a[t][c])<egg) continue;
        
        for(int i=c;i<=n;i++){//把这一列最大的一行换到最上面
            swap(a[r][i],a[t][i]);
        }
        for(int i=n;i>=c;i--){//把这一行的第一个数变成1，要倒着来
            a[r][i]/=a[r][c];
        }
        for(int i=r+1;i<n;i++){//把所有行的第c列消成0
            for(int j=n;j>=c;j--){
                a[i][j]-=a[r][j]*a[i][c];
            }
        }
        r++;
    }
    if(r<n){//剩下方程的个数<n
        for(int i=r;i<n;i++){
            if(fabs(a[i][n])>egg) return -1;//0=b,说明无解
        }
        return 1;//又无穷多组解
    }
    if(n>1){
        for(int i=n-2;i>=0;i--){
            for(int j=i+1;j<n;j++){
                a[i][n]-=a[i][j]*a[j][n];//推出解
            }
        }
    }
    return 0;
    
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<=n;j++){
            scanf("%lf",&a[i][j]);
        }
    }
    int t=gause();
    if(t==-1) puts("No solution");
    else if(t==1) puts("Infinite group solutions");
    else{
        for(int i=0;i<n;i++) printf("%.2lf\n",a[i][n]);
    }

求组合数

组数 a,b范围 处理方式
10万组 （1，2000） 递推
1万组 （1，100000） 预处理阶乘
20组 （1，200000） 卢卡斯定理

Ca^b^=a*(a-1)*…*(a-b+1)/(1*2*…*b)=(a!)/(b!)/(a-b!)

Ca^b^=Ca-1^b^+Ca-1^b-1^//从a个苹果选b个，不包含某一个苹果，包含某一个苹果

递推

0<a,b<2000, 100000组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<iostream>
using namespace std;
const int mod=1e9+7;
const int N=2010;
long long f[N][N];
int main(){
    int n;
    cin>>n;
    for(int i=0;i<N;i++){//预处理
        for(int j=0;j<=i;j++){
            if(!j)
            {
                f[i][j]=1;
            }
            else f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
        }
    }
    while(n--){
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%lld\n",f[a][b]);
    }
}

预处理

1≤a,b≤100000 10000组

预处理阶乘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=1e9+7;
ll fact[N],infact[N];
ll qmi(int a,int k,int p){//快速幂
    ll res=1;
    while(k){
        if(k&1) res=(ll)res*a%p;
    a=(ll)a*a%p;
    k>>=1;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    fact[0]=infact[0]=1;//0的阶乘是1
   
    for(int i=1;i<N;i++){
        fact[i]=(ll)i*fact[i-1]%mod;//1e9要用long long
        infact[i]=(ll)infact[i-1]*qmi(i,mod-2,mod)%mod;//(i!)^(-1),表示i的阶乘的逆元
    }
  
    while(n--){
        int a,b;
        cin>>a>>b;
        cout<<(ll)fact[a]*infact[a-b]%mod*infact[b]%mod<<endl;//3个数相乘会溢出，所以要mod
    }
    return 0;
}

卢卡斯定理

20组 1≤a,b≤1e18

Ca^b^ % p=Camodp^bmodp^*Ca/p^b/p^

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
ll pmi(int a,int k,int p){
    int res=1;
    while(k){
        if(k&1) res=(ll)res*a%p;
        a=(ll)a*a%p;
        k=k>>1;
    }
    return res;
}
ll C(ll a,ll b,ll p)
{
    if(b>a) {
        return 0;
    }
    int res=1;
    if(b>=1){
        for(int i=a,j=b;j>=1;j--,i--){
        res=(ll)res*i%p;
        res=(ll)res*pmi(j,p-2,p)%p;
    }
    return res;
    }
    return 1;
}
int ludas(ll a,ll b,ll p){
    if(a<p&&b<p){
        return (ll)C(a,b,p)%p;
    }
    else return (ll)C(a%p,b%p,p)*ludas(a/p,b/p,p)%p;
}
int main(){
    int n;
    cin>>n;
    while(n--){
        ll a,b,p;
        cin>>a>>b>>p;
        cout<<ludas(a,b,p)<<endl;
    }
    return 0;
}

高精度

  1. 找出质数
  2. 分解质因数
    • a!=p的倍数个数+p^2^的倍数个数+p^3^的倍数个数+…+p^k^的倍数个数
  3. 高精度乘法把因子乘到一起
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=5010;
bool st[N];
int pri[N],cnt,sum[N];
void prime(int x){//预处理1~a中所有的质数
    for(int i=2;i<=x;i++){
        if(!st[i]) pri[cnt++]=i;
    
    for(int j=0;pri[j]<=x/i;j++){
        st[i*pri[j]]=true;
        if(i%pri[j]==0) break;
    }
    }    
    
}
int get(int x,int p){
    int res=0;
    while(x!=0){
        res=res+x/p;
        x=x/p;
        //cout<<x<<endl;
    }
    return res;
}
vector<int> mul(vector<int> a,int b){//高精度乘法
    int t=0;
    vector<int> c;
    for(int i=0;i<a.size()||t;i++){
       if(i<a.size())  t=t+a[i]*b;
        c.push_back(t%10);
        t=t/10;
    }
    while(c.size()>1&&c.back()==0) c.pop_back();
    return c;
}
int main(){
    int a,b;
    cin>>a>>b;
    prime(a);
    for(int i=0;i<cnt;i++){
        int p=pri[i];
        sum[i]=get(a,p)-get(b,p)-get(a-b,p);
    }
    vector<int> res;
    res.push_back(1);
    for(int i=0;i<cnt;i++){
        for(int j=0;j<sum[i];j++){
            res=mul(res,pri[i]);
        }
    }
    for(int i=res.size()-1;i>=0;i--){
        printf("%d",res[i]);
    }
    return 0;
}

满足条件的01序列（卡特兰数）

给定 n个0和n个1，它们将按照某种顺序排成长度为2n的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个。

转化成从原点走路径的问题

从(0,0)走到(6,6)的问题，0是向上走一格，1是向上走一格

每个序列转化成从前往后走的路径，满足任意时刻，上走个数>右走个数，即x≥y

所有的路径的点必须在绿线上方，不经过红色边

所有走法：C12^6^

所有经过红色线的，在第一次经过时，按照红色做轴对称，终点是(5,7)，走法数为C12^5^

答案：C12^6^-C12^5^

C2n^n^-C2n^n-1^=C2n^n^/(n+1)->卡特兰数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
int qmi(int a,int k,int p){
    int res=1;
    while(k){
        if(k&1) res=(ll)res*a%p;
        a=(ll)a*a%p;
        k=k>>1;
    }
    return res;
}
const int mod=1e9+7;
int main(){
    int n;
    cin>>n;
    int res=1;
    for(int i=n+1;i<=2*n;i++){
        res=(ll)res*i%mod;
    }
    for(int i=1;i<=n+1;i++){
        res=(ll)res*qmi(i,mod-2,mod)%mod;//取模的数是质数，因此可以用费马小定理，否则只能用扩展欧几里得球逆元
    }
    cout<<res;
    return 0;
}

容斥原理

S=S1+S2+S3-S4-S5-S6+S7

Cn^1^+Cn^2^+…+Cn^n^=2^n^-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=20;
int p[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++) cin>>p[i];//读入质数
    int res=0;
    for(int i=1;i<1<<m;i++){
        int s=0;
        int t=1;
        for(int j=0;j<m;j++){
            if(i>>j&1){
                if((ll)p[j]*t>n){//看成二进制数，0表示不被选，1表示被选
                    t=-1;
                    break;
                }
                t=t*p[j];
                s++;
            }
        }
        if(t==-1) continue;
        if(s&1) res=res+n/t;
        else res=res-n/t;
    }
    cout<<res;
    return 0;
}

Nim游戏（博弈论）

Nim游戏

给定n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

必败态：（先手）走不到任何一个必败状态
必胜态：让剩下的状态变成必败态

  1. 0^0^0…^0=0

  2. 若a1^a2^..ai…^an!=x !=0
    x的二进制表示中，最高位为第k位，必然存在至少一个数ai，第k位二进制数位1(如果都是0，不可能出来x)
    ai^x<ai
    从ai拿走ai-ai^x个石子，剩下个ai^x个
    a1^a2^..ai^x…^an!=x^x=0

  3. 若a1^a2^..ai…^an!=x =0
    不管怎么拿，结局的异或值!=0

    要是为0，那么ai^ai‘=0,ai=ai,说明没拿走，不符合规则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
    int n;
    scanf("%d",&n);
    int res=0;
    int x;
    while(n--){
        scanf("%d",&x);
        res=res^x;
    }
    if(res!=0) puts("Yes");
    else puts("No");
    return 0;
}

台阶-Nim

现在，有一个n级台阶的楼梯，每级台阶上都有若干个石子，其中第i级台阶上有a^i^个石子(i≥1)。两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

  1. 奇数级台阶，若a1^a3^..ai…^an!=x !=0（偶数级台阶只需要重复对方步骤即可，奇数级台阶不变）

    • x!=0，则

  2. 奇数级台阶，若a1^a3^..ai…^an!=x=0，永远无法翻身

集合-Nim（SG函数）

mex运算：找到集合当中最小的不存在的自然数

SG(终点)=0
SG(x)=mex(SG(y1),SG(y2)…SG(yk))

重点状态（必败态）：SG(x)=0
若SG(x)!=0，证明可以到0，则说明是必胜态

很多图时，SG(x1)^SG(x2)…^SG(xn)=0 必败;SG(x1)^SG(x2)…^SG(xn) !=0必胜

证明： 所有SG(xi)都为0，则SG(x1)^SG(x2)…^SG(xn)=0，必败
SG(x1)^SG(x2)…^SG(xn )=x !=0一定可以找到SG(xi)^x < SG(xi),证明可以把这个局面变成0
SG(x1)^SG(x2)…^SG(xn )=x=0，不管怎么走，亦或出来不是0

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合S，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

SG(10)求法如图所示，也可以求出SG(7) SG(5)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<algorithm>
#include<set>
#include<cstring>
const int N=110,M=10010;
int s[N],m,n,f[M];
using namespace std;
int sg(int x){
    if(f[x]!=-1) return f[x];
    set<int> S;
    for(int i=0;i<m;i++){
        int sum=s[i];
        if(sum<=x) S.insert(sg(x-s[i]));
    }
    for(int i=0;;i++){
        if(!S.count(i)) return f[x]=i;//寻找不存在的最小的数
    }
    
}
int main(){
    cin>>m;
    memset(f,-1,sizeof f);
    for(int i=0;i<m;i++){//读入m个
        cin>>s[i];
    }
    cin>>n;
    int res=0;
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        res=res^sg(x);
    }
    if(res==0) puts("No");
    else puts("Yes");
    return 0;
}

拆分Nim

给定n堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为0，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_set>//存储可以到的局面
using namespace std;
const int N=110;
unordered_set<int> S;
int f[N];//每一个值的SG值
int sg(int x){
    if(f[x]!=-1) return f[x];//说明被计算过了
    for(int i=0;i<x;i++){
        for(int j=0;j<=i;j++){
            S.insert(sg(i) ^ sg(j));//取走任意一堆之后，增加两堆新的
        }
    }
    for(int i=0;;i++){//mex操作，找不存在的最小自然数
        if(!S.count(i)) return f[x]=i;
    }
}
int main(){
    int n;
    cin>>n;//石子堆数
    memset(f,-1,sizeof f);//所有SG>0
    int res=0;
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        res=res^sg(x);
    }
    if(res) puts("Yes");
    else puts("No");
    return 0;
}