快速排序

  • 思想：分治

  1. 确定分界点：q[l]/ q[(l+r)/2] /q[r] /随机

  2. ==（难点）==调整区间：≤x x ≥x

  3. 递归处理左右两段

    暴力做法：

    • 设置a[],b[]
    • 对于q[l~r]:
      • q[i]≤x,x->a[]
      • q[i]≥x,x->b[]
    • a[]->q[],b[]->q[]

    优美做法：

    • 设置双指针l,r
      • i往右移动，直到看到≥x的数
      • j往左移动，直到看到≤x的数
      • swap（i,j)
      • 循环，直到i,j相遇
1
2
3
4
5
6
7
8
9
10
11
12
13
void quick_sort(int q[],int l,int r)
{
    if(l>=r) return;//判边界，如果只有一个数/没有数直接返回
    int i=l-1,j=r+1,x=q[l];
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    quick_sort(q,l,j);//可以写i-1,相应下行写成i,应该是x=q[(1+l+r)/2],写x=q[l]会死循环。样例：1,2
    quick_sort(q,j+1,r);//用j时，不能写x=q[r]
}

归并排序 ==O(n*lgn)==

  • 思想：分治
    1. 确定分界点mid=(l+r)/2
    2. 递归排序left、right
    3. 归并，合二为一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void merge_sort(int q[],int l,int r)
{
    if(l>=r) return;
    int i=l,k=0,mid=(l+r)>>1;
    int j=mid+1;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    while(i<=mid&&j<=r)
    {
        if(q[i]<=q[j]) tmp[k++]=q[i++];
        else tmp[k++]=q[j++];
    }
    while(i<=mid) tmp[k++]=q[i++];
    while(j<=r) tmp[k++]=q[j++];
    for(i=l,j=0;i<=r;i++,j++)
    {
        q[i]=tmp[j];
    }
}

二分

  • 整数二分(二分左边）：
    1. mid=(l+r==+1==)/2//l=mid，补上+1
    2. if(check(mid))
      • true->[mid,r]//若l=r-1，如果mid=(l+r)/2，此处死循环
      • flase->[l,mid-1]

  • 整数二分(二分右边）：

    1. mid=(l+r)/2//r=mid，无需补上+1

    2. if(check(mid))

      • true->[l,mid]

      • flase->[mid+1,r]

高精度（位数1e6)

高精度加法

  1. 大整数存储

    方式：用数组存储，==第0位存个位==（目的是方便进位）

    比如，输入：123456789

    a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8]
    9 8 7 6 5 4 3 2 1

    往后输入直接push_back即可

  2. 运算过程

    模拟人工加法，先加个位数，进位，再加十位数……

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    vector<int> add(vector<int> &A,vector<int> &B){
        if(A.size()<B.size()) return add(B,A);
        vector<int> C;
        int t=0;
        for(int i=0;i<A.size();i++){
            t+=A[i];
            if(i<B.size()) t+=B[i];
            C.push_bzack(t%10);
            t=t/10;
        }
        if(t) C.push_back(t);
        return C;
    }

高精度减法

  1. A≥B， 算A-B
  2. A<B，算-(B-A)
1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> sub(vector<int> &A,vector<int> &B){
    vector<int> C;
    int t=0;
    for(int i=0,t=0;i<A.size();i++){
        t=A[i]-t;
        if(i<B.size()) t=t-B[i];
        C.push_back((t+10)%10);
        if(t<0) t=1;
        else t=0;
    }
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

高精度乘法

适用于高精度整数*低精度整数

1
2
3
4
5
6
7
8
9
10
vector<int> mul(vector<int> &A,int b){
    int t=0;
    vector<int> C;
    for(int i=0;i<A.size()||t!=0;i++){
        if(i<A.size()) t+=A[i]*b;
        C.push_back(t%10);
        t=t/10;
    }
    return C;
}

高精度除法

适用于高精度整数/低精度整数

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> div(vector<int> &A,int b,int &r){//r通过引用传回去
    vector<int> C;
    r=0;
    for(int i=A.size()-1;i>=0;i--){//注意要从高位开始算
        r=r*10+A[i];
        C.push_back(r/b);//注意是/b
        r=r%b;
    }
    reverse(C.begin(),C.end());//恢复前面的规则，即个位存储在C[0]
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

前缀和

有一个数组a1,a2,a3,a4,a5,……

  1. 前缀和Si=a1+a2+a3+a4+a5……+ai

    求法：Si=Si+1+ai

  2. 作用：可以快速求出数组里面某一段的和：Sr-Sl-1

子矩阵的和（二维前缀和）

  1. S[i,j]的含义：

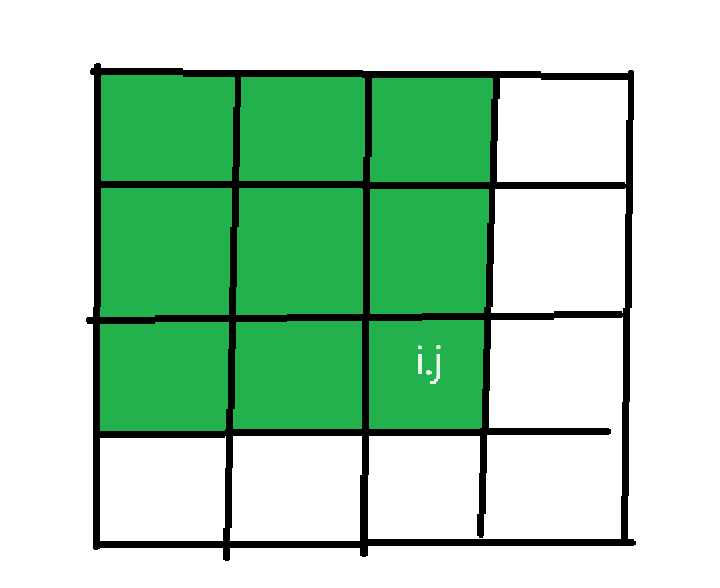
  2. (x1,y1),(x2,y2)这一子矩阵的和该如何计算？

    • S[x2,y2]-S[x2,y1-1]-S[x1-1,y2]+S[x1-1,y1-1]

  3. S[i,j]如何计算？

    • S[i,j]=S[i-1,j]+S[i,j-1]-S[i-1,j-1]+a[i,j]
    • 按照每一行从左往右求
    • 下标从1开始计算

差分

对于a1,a2,……an

构造b1,b2,……bn;

使得ai=b1+b2+……+bn;b成为a的差分，a为b的前缀和

适用于：使a[l,r]上的数字全部加上c->仅需让bl+c，br+1-c

注意：不需要插入ai，只需要看成i到i插入ai即可

差分矩阵（二位差分）

对于a[n,m]，假想一个b[n,m]，使得a数组为b数组的前缀和

适用于：从(x1,y1)到（x2,y2)的部分加上c，仅需b[x1,y1]+=c,b[x2+1,y1]-=c,b[x2+1,y1]-=c,b[x2+1,y2+1]+=c;

注意：不需特意构造b[i,j]，只需要看成i,j到i,j插入a[i,j]即可

最长连续不重复子序列

双指针算法模板：

1
2
3
for(int i=0,j=0;i<n;i++){
	while(j<i&&check(i,j)) j++;
}

双指针算法用途：优化复杂度到 O(n)

位运算操作

  1. 整数n的二进制表示里面第k位数字是几

    • n=15=(1111)2

    先把第k位移到个位，即n右移k位，看个位是几；n>>k&1

  2. lowbit(x)返回x的最后一位1：

1
2
x=1010;
则lowbit(x)=10;

原理：x&(-x)

应用：求x中1的个数

离散化（整数，保序）

a[]={1，3,100,2000,500000};

映射到0,1,2,3,4

  1. a中可能有重复元素，需要去重
  2. 如何算出x在a中的下标？ 用二分

适用于：数据范围很大，但是很稀疏

==去重==：

1
alls.erase(unique(all.begin(),alls.end()),alls.end());

unique：重复元素移到末尾，并且返回重复元素开始的端点

区间合并

把有交集的区间合并成为一个区间（有公共端点也合并）

  1. 按照区间的左端点排序
  2. 扫描整个区间，扫描的过程中，合并区间